Motiver la définition d'écart-type
Quand on commence à parler de dispersion des données aux élèves, on arrive vite à leur présenter la star du domaine, j’ai nommé…
l’écart-type!1
\[\sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2}\]
C’est pas très beau, hein? 😬️ Alors, pourquoi s’embête-t-on avec cette définition?
On peut toujours commencer par montrer qu’elle a l’air de mesurer ce qu’il faut: quand toutes les données sont égales à la moyenne, l’écart-type est nul. Et plus les données sont éloignées de la moyenne, plus l’écart-type va augmenter. Donc on sent qu’un jeu de données avec un grand écart-type devrait être plus dispersé qu’un jeu de données avec un petit 👌️
Mais sérieusement, pourquoi ne pas prendre un truc plus simple, comme la moyenne des écarts \[\frac{1}{n} \sum_{i=1}^n \lvert x_i - \bar{x}\rvert\] ou l’écart interquartile?
Et surtout, comment interpréter la valeur de l’écart-type? Si on dit qu’une donnée est dans l’intervalle interquartile, ça veut dire qu’elle est dans la moitié des observations centrales, mais éloigné de la moyenne d’1 fois l’écart-type, ça veut dire quoi?
Quand on fait des maths à un certain niveau, on se rend bien compte que cette définition fait sens, qu’elle s’inscrit dans un écosystème (normes Lp, moments d’une variable aléatoire…). Mais je me demandais s’il y avait des raisons plus spécifiques. Du coup, j’ai fait un peu de recherches sur ce sujet 🕵️🔎
Et… la seule réponse que j’ai trouvée ne va pas vraiment plus loin: c’est une définition qui fonctionne bien, qui est riche mathématiquement. Elle se prête bien à la construction de théorèmes. En revanche, on ne tire pas grand chose de l’écart moyen ou des quartiles ☹️
Mais va-t-en expliquer ça à un élève 🙄️
Mon approche actuellement, c’est de développer la notion de dispersion à travers les quartiles d’abord. Leur interprétation est beaucoup plus transparente.
Ensuite, je dis que les quartiles, c’est top, mais on ne sait rien en faire math. Du coup, on a pondu autre chose: l’écart-type. Et regardez, sur une gaussienne, ça comprend 68% des données autour de la moyenne!2

Donc si l’écart-type est plus grand, la gaussienne sera plus étalée, etc. J’en profite alors aussi pour lier le concept avec une boite à moustaches:3
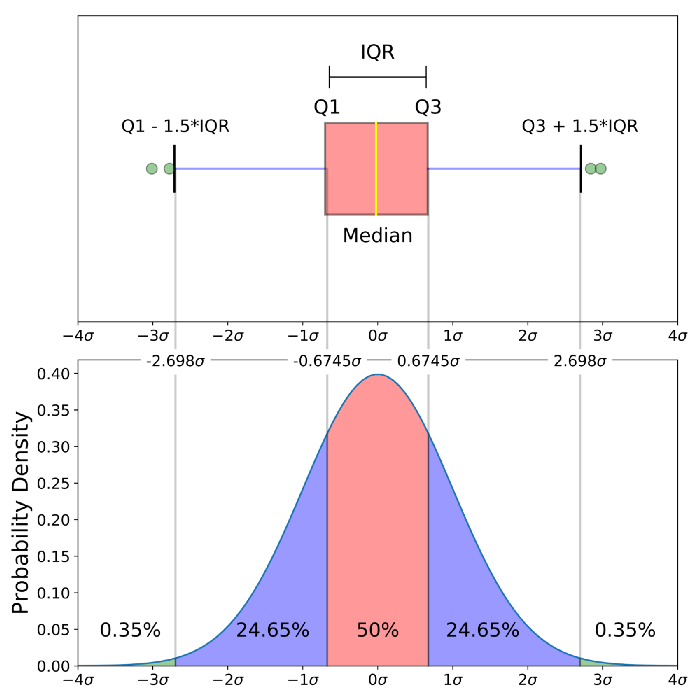
Le but ici, c’est surtout de montrer que oui, l’écart-type mesure la même chose que l’écart interquartile, et que donc on peut transférer l’intuition qu’on a acquise, même si, en général, la valeur de l’écart-type n’a pas d’interprétation directe.
Pour terminer, je mentionne tout de même qu’on peut aussi donner du sens à l’écart-type grâce à l’inégalité de Tchebychev:
\[P(\lvert X - \mu\rvert \geq \alpha) \leq \frac{\sigma^2}{\alpha}\] pour tout \(\alpha>0\), avec \(\mu\) la moyenne et \(\sigma\) l’écart-type.
Ça donne des infos pour n’importe quelle distribution, mais soyons honnêtes, ce n’est pas si facile à interpréter non plus, surtout pour un élève.
Tandis que l’image de la gaussienne, c’est précis, c’est facile, c’est top 👍️
Photo-bannière de Oksana Taran sur Unsplash.